Inecuaciones

1.  Una representación gráfica. 
2.  Un intervalo

Un ejemplo que no puede ayudar a entender estas dos representaciones de una inecución es:

 

Considere la inecuación 2x-1<7

Para resolver la inecuación realizamos pasos semejantes a los de una ecuación, primero al añadir uno a ambos lados de la inecuación se tiene que:  

2x-1+1<7+1   y la inecuación conserva su relación 

de lo anterior se tiene que 2x<8, y se puede multiplicar por un medio (o dividir por dos) haciendo asi lo siguiente:

2x(1/2)<8(1/2)  lo cual es equivalente a  (2x)/2< (8)/2 teniendo un resultado final de x<4.

Ahora este resultado se puede representar en una recta númerica de la siguiente manera:

 

                                             

Para expresar la respuesta en forma de intervalo se debe notar que el menor número que se encuentra sobre la semirecta verde es el -∞ (recordemos que no es un número sino una interpretación) y el mayor es el número 4, dado que la relación esta dada por el "menor que" el intervalo no incluye al número 4, teniendo como respuesta el siguiente intervalo:   (-∞,4)

 

Si modificaramos la inecuación inicial para que sea  2x-1<7, quedaria (aplicando los mismos procesos) que:

x< 4  y de este modo la imagen queda definida de la siguiente manera:

                                                

y en forma de intervalo queda dofinido como  (-∞,4] cerrando con corchetes el intervalo, puesto que se usa la relación "menor o igual"

Finalmente si cambiamos la inecuación por las siguientes 2x-1>7 y 2x-1>7 se obtienen resultados muy parecidos, puesto que el algoritmo es el mismo, se mostrarán los resultados.

Para la inecuación 2x-1>7, resolviendola queda como x>4 y sus respectivas representaciones son:

                                                  

(4,+∞) en forma de intervalo.

 

Para la inecuación  2x-1>7, su solución es x>4 y sus respectivas representaciones son:

                                                   

[4,+∞) en forma de intervalo.

1. Quitar corchetes y paréntesis.
2. Quitar denominadores.
3. Agrupar los términos en x a un lado de la desigualdad y los términos independientes en el otro.
4. Efectuar las operaciones.
5. Si el coeficiente de la x es negativo multiplicamos por −1, por lo que cambiará el sentido de la desigualdad.
6. Despejamos la incógnita.
7. Expresar la solución de forma gráfica y con un intervalo.

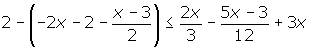
Si empezamos aplicando los pasos, quitamos los parentesis aplicando ley de los signos  

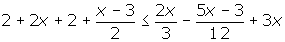
luego se quitan los denominadores así:

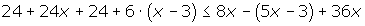
Dado que el procedimiento anterior nos deja unos parentesis volvemos a quitar los parentesis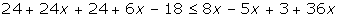

luego se agrupan  las variables en un lado de la desigualdad:

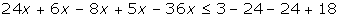
se reducen los terminos semejantes:

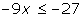
Y finalmente se despeja la variable de la inecuación

x>3

la representación gráfica se puede mostrar así:

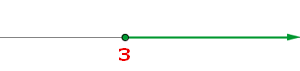
De forma en intervalo se muestra así: [3,+∞)

Inecuaciones de segundo grado

Consideremos la inecuación:   x² − 6x + 8 > 0 

La resolveremos aplicando los siguientes pasos:

1. Igualamos el polinomio del primer miembro a cero y obtenemos las raíces de la ecuación de segundo grado:      x² − 6x + 8 = 0   

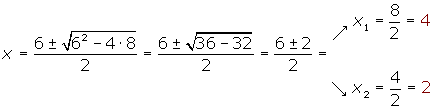
2.   Representamos estos valores en la recta real. Tomamos un punto de cada intervalo y evaluamos el signo en cada intervalo 

 P(0) = 0² − 6 · 0 + 8 > 0

P(3) = 3² − 6 · 3 + 8 = 17 − 18 < 0

P(5) = 5² − 6 · 5 + 8 = 33 − 30 > 0

3.La solución está compuesta por los intervalos (o el intervalo) que tengan el mismo signo que el polinomio.

S = (-∞, 2) U (4, ∞)

x² + 2x +1 ≥ 0

x² + 2x +1 = 0

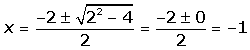
(x + 1)² ≥ 0

Como un número elevado al cuadrado es siempre positivo la solución es R

		Solución
x2 + 2x +1 ≥ 0	(x + 1)2 ≥ 0
x2 + 2x +1 > 0	(x + 1)2 > 0
x2 + 2x +1 ≤ 0	(x + 1)2 ≤ 0	x = − 1
x2 + 2x +1 < 0	(x + 1)2 < 0

x² + x +1 > 0

x² + x +1 = 0

Cuando no tiene raíces reales, le damos al polinomio cualquier valor si:

El signo obtenido coincide con el de la desigualdad, la solución es R.

El signo obtenido no coincide con el de la desigualdad, no tiene solución.

	Solución
x2 + x +1 ≥ 0
x2 + x +1 > 0
x2 + x +1 ≤ 0
x2 + x +1 < 0

Inecuaciones racionales

Las inecuaciones racionales se resuelven de un modo similar a las de segundo grado, pero hay que tener presente que el denominador no puede ser cero

1. Hallamos las raíces del numerador y del denominador

x − 2 = 0      x = 2

x − 4 = 0      x = 4

2. Representamos estos valores en la recta real, teniendo en cuenta que las raíces del denominador, independientemente del signo de la desigualdad, tienen que ser abiertas

Tomamos un punto de cada intervalo y evaluamos el signo en cada intervalo

4. La solución está compuesta por los intervalos (o el intervalo) que tengan el mismo signo que la fracción polinómica

S = (-∞, 2] U (4, ∞)

Pasamos el 2 al primer miembro y ponemos a común denominador.

Hallamos las raíces del numerador y del denominador.

−x + 7 = 0      x = 7

x − 2 = 0        x = 2

Evaluamos el signo:

S = (-∞, 2) U (7, ∞)